CONDITION FOR S-BOX TO BE INVERTIBLE
Since for a 2 2 matrix A there exists another square matrix B of size 2 2 such that AB BAI 2 2 the matrix A is invertible. A is row-equivalent to the n n identity matrix I_n.

Restricting Domains Of Functions To Make Them Invertible Video Khan Academy
However in this case the condition for a square matrix to be invertible is that its determinant is invertible in the ring which in general is a much stricter requirement than being nonzero.

. If θ2 1 and θ1 θ2 1 then the MA2 process is invertible. For the Box-Jenkins model 1 to be invertible it must be the case that all of the roots of the moving average polynomial must be greater than one in magnitude or if complex have modulus greater than one. Matrix inversion is the process of finding the matrix B that satisfies the prior equation for a given invertible matrix.
True or false with a counterexample if false and a reason if true. 1 Answer to 1. 2 c Define a trapdoor one-way function and explain its use in asymmetric-key cryptography.
Any square matrix A over a field R is invertible if and only if any of the following equivalent conditionsand hence all hold true. The matrix A has a left inverse that is there exists a B such that BA I or a right inverse that is. Falconers Formula for the Hausdorff Dimension of a SelfAffine Set in R2 Irene Hueter Purdue University Steven P.
Definition of Invertible Matrix. The condition for invertibility of a MA1 process is the counterpart to the condition of stationarity of an AR1 process. Up to 10 cash back This requires S 1 H to be diagonal since c is the diagonalising matrix.
A A 4 times 4 matrix with a row of zeros is not invertible. 2 e List the services provided by SSL. The invertible architecture transforms the latent space z that is concatenated at different scales to the input x conditioned on c l L l 1 where L is number of invertible blocks.
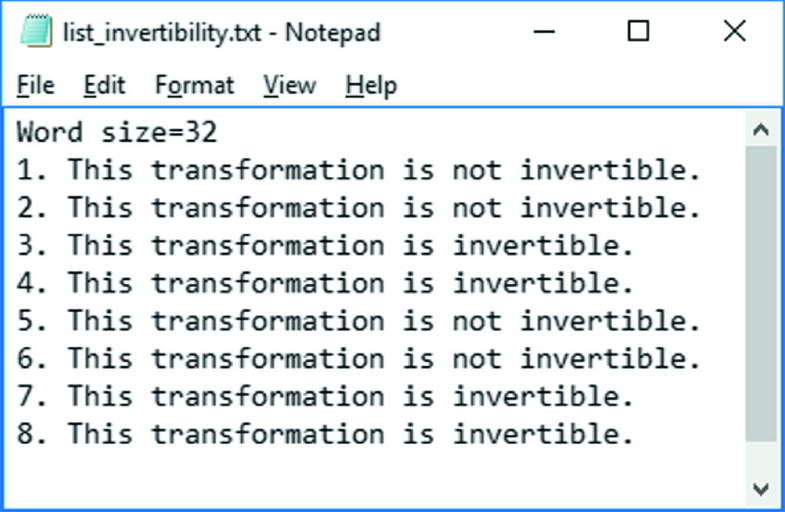
Define an S-box and mention the necessary condition for an S-box to be invertible. Suppose Ax λx with x0. Strict Avalanche Criteria Informally if one bit input is changed in an S-Box then half of the output bits should be changed For a function f to satisfy SAC the following condition is satisfied.
A matrix A of dimension n x n is called invertible only under the condition if there exists another matrix B of the same dimension such that AB BA I where I is the identity matrix of the same order. In this work we construct 4 invertible blocks with the first three blocks being convolutional invertible blocks and the last invertible block being a fully-connected block. The following statements are equivalent ie they are either all true or all false for any given matrix.
Produce 4 x 4 substitution boxes. Co-efficient matrix T adjA Step 3. Let α be a scalar different from the eigenvalues of A and let B AαI1.
Let A be a square n by n matrix over a field K eg the field R of real numbers. S-Boxs are invertible. The invertible matrix theorem is a theorem in linear algebra which offers a list of equivalent conditions for an nn square matrix A to have an inverse.
Obtain the inverse matrix. That is an ARprocess. It is a known theorem that if A is invertible then Upper A Superscript negative 1 must also be invertible.
It turns out that if θ1 1 then this infinite series converges to a finite value. Use this equation to find an eigenvalue of A in terms of μ and α. Note that μ 0 because B is invertible.
Lalley Purdue University March 1993 Abstract Simple sufficient conditions are given for the validity of a formula of Falconer 3 describing the Hausdorffdimension ofa self-affine set. 54 maps to 43 in the S-box 42 maps to 64 in. An S-box can be invertible if the number of input bits is same as the number of output bits.
65 DES function The heart of DES is the DES function. 3 d Define the first and second criterion for a cryptographic hash functions. Let rst introduce the notation a which.
According to the Invertible Matrix Theorem if a matrix is invertible its columns form a linearly independent set. Therefore the columns of Upper A. In such a case matrix B is known as the inverse of matrix A.
The DES function applies a 48-bit key to the rightmost 32 bits R I1 to produce a 32-bit output. These conditions are natural and. What is the difference between Linear Non-Linear S- Boxes.
Invertible matrix Non-linearity of f and g are same. List some components of a modem block cipher. An S-box Substitution box can be thought of as a miniature substitution cipher.
The inverse S-box is simply the S-box run in reverse. Define a P-box and list its three variations. Properties The invertible matrix theorem.
Define a S-Box and mention the necessary condition for a S-Box to be invertible. A well known example is the 8-bit S-box S used in RIJNDAEL 5. Which variation is invertible.
Invertibility An S-box may or may not be invertible. I f It is a necessary but not sufficient condition if the S-boxes formed from the j single output bit functions are to be invertible. This function is made up of four sections.
Suppose μ is an eigenvalue of B and that x is a corresponding eigenvector so that AαI1x μx. Such MAq processes are called invertible. A potentially invertible function returns a value i of 1 for one half of the possible input vectors and a value of 0 for the other half.
Obtain the adjoint of the matrix. If y t y t 1 t. B Define an S-box and mention the necessary condition for an S-box to be invertible.
Although this number might seem surprisingly high at rst in 3 it is shown that it can easily be explained from the special algebraic structure of the S-box of RIJNDAEL and it can be generalized for the inversion in GF2n. Inverse of matrix A is symbolically. The 12870 potentially invertible.
If θ1 1 then the MA1 process is invertible. An expansion D-box a. It has 2040 di erent self-equivalence relations.
B Every matrix with. Since detA is not equal to zero A is invertible. S S S S S S S S Straight D-box Expansion D-box S-Boxes XOR 32 bits In 48 bits 32 bits 32 bits Fig.
A MA1 representation with coe cients s sMore generally invertibility of an MAq process is the ip side of stationarity of an ARp process. There is an n-by-n matrix B such that AB I n BA. Look at the Wikipedia example.
00 maps to 63 in the S-box 63 maps to 00 in the inverse S-Box. One way to calculate the inverse of an S-box is. Then j j s.
Specifically this condition is satisfied in cases when S and H are both diagonal implying that the configurations are mutually orthogonal diagonal S and there is no interaction between the configurations diagonal H. In an invertible S-box the number of input bits should be the same as the number of output bits. Check the condition ABBAI.
All you need to use the S-Box itself to find an elements inverse.

Pdf Construction Of S Box Based On Mobius Transformation And Increasing Its Confusion Creating Ability Through Invertible Function

New Slim Women Winter Thicken Warm Fleece Lined Thermal Stretchy Leggings Pants Ebay Warm Leggings Leggings Are Not Pants Fleece Leggings

Inverse Functions Domain Range With Fractions Square Roots Graphs Youtube

Determining Invertible Matrices Video Khan Academy

Definition Of Invertible Matrix Chegg Com
Analysis Of Rotation Based Diffusion Functions Springerlink

Hexyflex Kinetic Wire Sculpture Moving Hexagon Flexable Invertible Cube Schatz Ebay
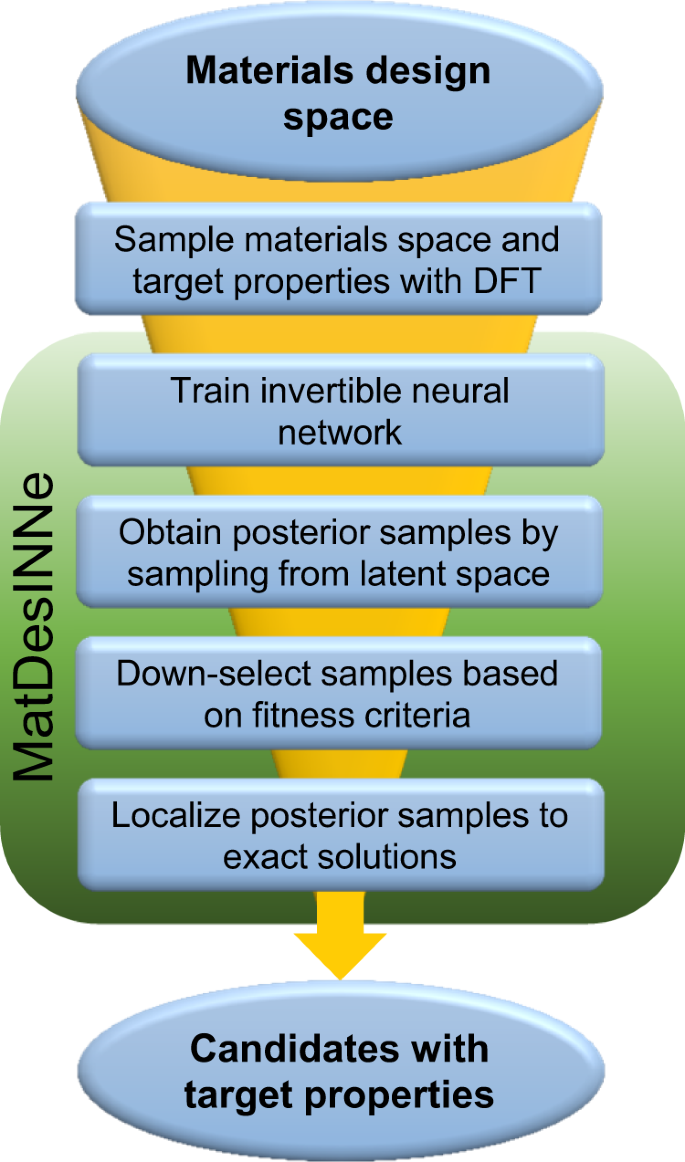
Inverse Design Of Two Dimensional Materials With Invertible Neural Networks Npj Computational Materials

Belum ada Komentar untuk "CONDITION FOR S-BOX TO BE INVERTIBLE"
Posting Komentar